第8回 コロイド分散系の安定性評価とポテンシャル曲線
DLVO理論に従うと、対称型電解質水溶液中(価数z, 数密度n)において表面間距離Hにある半径αの2個のコロイド粒子間相互作用のポテンシャルエネルギーV(H)は静電斥力エネルギー(第6回 (2)式)とvan der Waals引力エネルギー(第2回図2右上)の和として次式で与えられる。
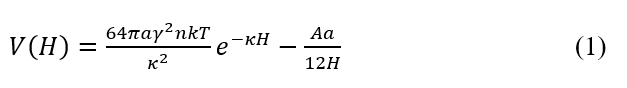
V(H)に高い山すなわち極大値Vmax(ポテンシャル障壁)が存在すれば、コロイド分散系は安定であり、そうでなければ系は不安定で凝集する。粒子の表面電位ψoが高いと(1)式の第1項(γ= tanh(zeψo/4kT)を通してψoに依存)が大きくなり、ポテンシャルの高い山が現れ、逆にHamaker定数Aが大きいと第2項が大きくなり高い山は現れない。ψoは分散促進因子であり、Aは凝集促進因子である。
図1にポテンシャル曲線がψoの変化とともにどのように変わるか計算例を示した。ψoの増大とともにVmaxは高くなるが、やがて最大値に達するとそれ以上高くならない。これは、ψoが小さいときはγはψoに比例して増加するが、ψoが大きくなるとγは1に飽和するからである(ψo→∞でγ→1)。後に述べるが、ここにDLVO理論の成功の鍵が隠されている。
極大の位置Hmと Vmax≡V(Hm)はLambertのW関数を用いて次式のように計算される1)。
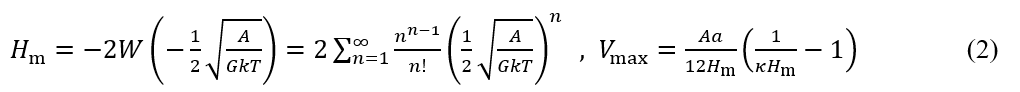
ただし、G= 384πγ2εrεokT/z2e2κである。GkT/A >exp(2)/4 (=1.8473) の場合にのみV(H)に極大が現れる。一般にVmax ≥ 15kTの場合、分散系は安定であるとみなされる。
図2にVmaxをψoとAの関数として3次元的に表した。凸部がVmax ≥ 15kTを満たす安定領域(分散)であり、平坦な部分はこの条件を満たさない不安定領域(凝集)である、図2はコロイド分散系の安定性を評価する3次元安定性マップである。
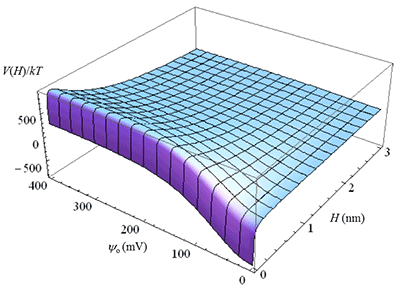 図1. コロイド粒子間相互作用に対するポテンシャル 曲線V(H)の表面電位ψo依存. α=0.1 mm, A=4×10-21 J, 25℃, z=1, 0.1 M水溶液 |
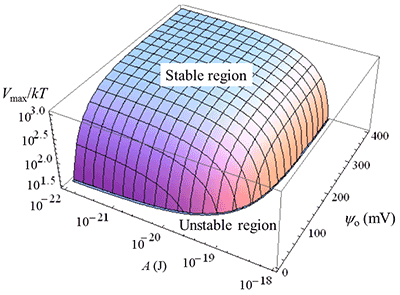 図2. 3次元安定性マップ. 凸部はVmax ≥ 15kTを満たす安定 領域.平坦部はVmax ≥ 15kTを満たす不安定領域. α=0.1 mm, A=4×10-21 J, 25℃, z=1, 0.1 M水溶液. |
文献: H. Ohshima, Approximate Analytic Expression for the Stability Ratio of Colloidal Dispersions, Colloid Polym. Sci., 292, 2269-2274 (2014).

