第50回　すべり表面をもつ粒子の電気泳動移動度

これまで界面動電現象の問題を解くとき、粒子表面で粒子に相対的な流体の速度をゼロと置く境界条件（すべりなし境界条件）を用いてきた。しかし、この境界条件は粒子表面の分子と媒質分子の間の分子間引力の強い親水性粒子の場合には正しいが、粒子表面―媒質間の分子間引力の弱い疎水性粒子の場合は厳密には正しくない。粘度ηの液体媒質中を運動する粒子を考えよう。粒子サイズがDebye長1/κ（κ=Debye-Hückelのパラメタ）より十分大きく粒子表面を平板とみなせるものとする。平板表面に垂直にx軸をとり原点0を平板表面に定める（図1）。

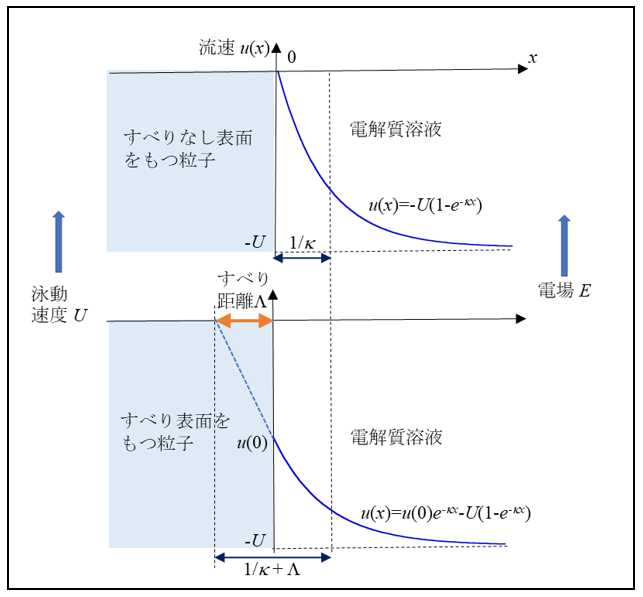
粒子表面における液体の相対速度u(x)に対するすべりなし境界条件はu(0)= 0である。すべりがある場合、u(0)はゼロではなく、βu(0)=ηdu/dx（=すべり摩擦力，β=すべり摩擦係数）、すなわち次式で与えられる。

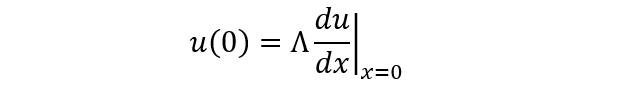　(1)
　

ここで、Λ=η/β はすべり距離とよばれる。Λ=0は親水性表面に対応し、Λが大きいほど粒子表面の疎水性が増大し、Λ=∞は完全な疎水性表面に対応する。境界条件(1)の下では電気泳動移動度は次式になる。

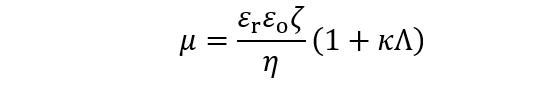　(2)

ここで、ε_r=電解質溶液の比誘電率、ε_o=真空の誘電率である。すべりなし表面をもつ粒子に対するSmoluchowskiの式μ=ε_rε_oζ/η（第20回コラム）と比較すると(1 + κΛ) 倍増加することがわかる。疎水性の非常に高い粒子では、この補正は無視できない。すべり距離Λの意味は次のように考えられる。図1のように、すべりがある場合、u(0)はゼロにならないが流速を表す曲線（青の実線）をそのまま粒子内部に仮想的に延長すると（青の点線）、u=0になる場所の位置がΛになる。これは、液体粒子（液滴）の場合（第30回コラム）、流速が液滴表面でゼロにならず、粒子内部に侵入したある場所でゼロになる状況と似ている。ただし、液滴では内部に液体の流れがあるが、すべり表面をもつ粒子の場合、“粒子内部で流速がゼロになる場所”というのはあくまで仮想的なものである。液滴（半径α，粘度η_d）電気泳動移動度の式でη/3η_d=Λ/αの置き換えをすると、半径α、すべり距離Λの球状粒子の電気泳動移動度の式が得られる。(2)式は以下のように導かれる。電場E中において速度Uで泳動する粒子表面における速度勾配の大きさdu/dxはU/(1/κ+Λ)にほぼ等しい（図1）。したがって、粒子表面に働く粘性力ηdu/dx（単位面積当たり）はηdu/dx=ηU/(1/κ+Λ)になる。一方、粒子表面の電荷密度をσとすると表面に働く電気力は単位面積当たりσEになる。粘性力と電気力がつり合うため、ηU/(1/κ+Λ)=σEである。このつり合いの式から、電気泳動移動度μ=U/Eはμ=σ/ηκのように得られる。この式に表面電荷密度σと表面電位ψ_oを結びつける式ψ_o=σ/ε_rε_oκを代入し、かつψ_o =ζと近似すると(2)式が得られる。