第7回 エネルギーの尺度:熱エネルギーとポテンシャル曲線
溶液中のイオンやコロイド粒子(粒子と総称)は互いに力を及ぼしながら、絶えず熱運動と呼ばれる無秩序な運動を行っている(コロイド粒子ではBrown運動)。粒子のエネルギーはポテンシャルエネルギーと熱運動の運動エネルギー(熱エネルギーと呼ぶ)の和である。熱エネルギーはkTで与えられる。ここで、kはBoltzmann定数 (k = 1.38×10-21J/K)、Tは絶対温度である。室温 (25℃= 298.15 K) ではkT = 4×10-21 J になる。粒子の挙動は粒子間に働く力で決まるが、力はベクトルなので、力よりも「力に逆らっている度合」(スカラーである)を扱う方が便利である。これがポテンシャルエネルギーである(ポテンシャルエネルギーの勾配にマイナスを付けた量が力になるように定義する)。なお、kTを電位の単位で表すと、室温で kT/e= 25 mVになる。
例として、互いにクーロン引力で引き合うNa+イオンとCl-イオンを考える。イオンが比誘電率εrの媒質中にあるとき、ポテンシャルエネルギーは V(R)=-e2/4πεrεoRになる(ただし、R= 2つのイオンの中心間距離)。クーロン引力に逆らってイオン同士が離れると(Rが大きくなると)V(R)は上昇し、逆にクーロン引力に従って接近するとV(R)は低下する。V(R)をRの関数として図示したものをポテンシャル曲線と呼ぶ。
図1は媒質が空気(εr= 1)および25℃の水(εr= 78.54)の場合の比較である。Rは2つのイオンの半径の和以下になれないので、この場所にポテンシャルの谷ができる。谷の深さがNa+とCl-の結合エネルギーになる。イオンは静止せずに激しい熱運動を行っているので、結合エネルギーが熱エネルギーkTより十分大きいとき、つまり、ポテンシャルの谷がkTより十分深いときに結合が安定であり、そうでなければ、Na+とCl-は結合できない。
媒質が空気の場合は、ポテンシャルの谷はkTの約200倍もあるのでNa+とCl-は互いに強く結合する。しかし、水の中では、εrが約80あってポテンシャルの谷は1/80に浅くなり、結合エネルギーはkTの約2.5倍程度にしかならず、Na+とCl-は解離してしまう。
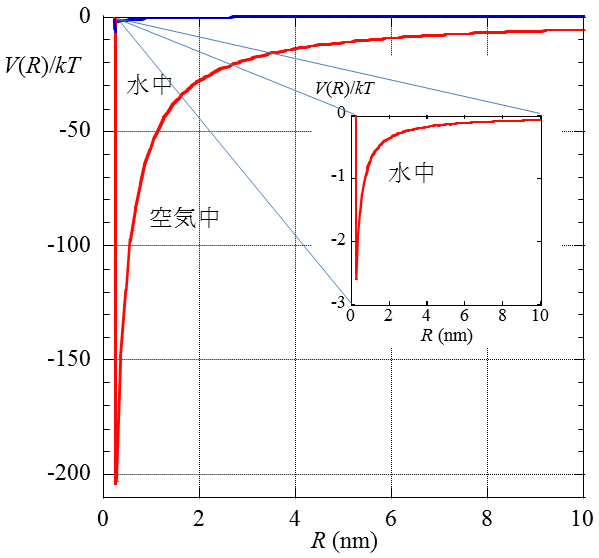
図1. Na+とCl-のクーロン引力相互作用に対するポテンシャル曲線
コロイド分散系の安定性に関するDLVO理論においてもポテンシャル曲線が用いられる。2個のコロイド粒子間相互作用のポテンシャルエネルギーはvan der Waals引力(第2回参照)と電気二重層の重なりに起因する静電斥力(第6回参照)のそれぞれのポテンシャルエネルギーの和で与えられ、2つのコロイド粒子間の表面間距離の関数になる。静電斥力が大きくポテンシャル曲線に熱エネルギーより高い山ができる場合は、コロイド粒子は凝集しにくい。逆に、van der Waals引力が大きい場合、ポテンシャル曲線にkTより高い山は現れず、コロイド粒子は容易に凝集する。詳しくは次回で解説する。

