第29回 液体膜上の電気浸透
球状粒子の半径が拡散電気二重層の厚さ(Debye長1/κ)よりも十分大きい場合、粒子表面の曲率を無視して平板とみなすことができる(図1)。電解質溶液中における平板状粒子の電気泳動と固定平板に接する電解質溶液の移動すなわち電気浸透は等価である。電気泳動速度と電気浸透速度は向きが逆で大きさは等しく、いずれもSmoluchowskiの式で与えられる。液滴の場合もこのような極限として、図1のように固体平板上に置いた油や水銀などの平らな表面をもつ液体膜を考える。液体膜に平行に電場Eをかけると、液体膜表面が帯電している場合、電解質溶液の電気浸透が起きる。
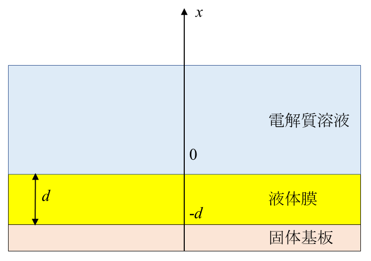
図1 電解質溶液と接する液体膜 (厚さd)
ここで、液体膜と電解質溶液の界面の電位が液体膜のゼータ電位ζである。液体膜と電解質溶液は混ざらないので、液体膜中にはイオンは存在しない。しかし、電解質溶液の流動は液体膜中に伝わり液体の流動が液体膜内に存在する。液体膜の下部に存在する固体表面で液体の流動は止む。
図2には、電場Eの下で厚さdの水銀の液体膜(粘度ηd=1.525mPa⸱s)が電解質水溶液(粘度ηd=0.891mPa⸱s)と接する場合の液体膜を横切る流速分布u(x)を固体表面の場合とともに与えた(縦軸の1目盛りはεrεoζE/ηを表す)。
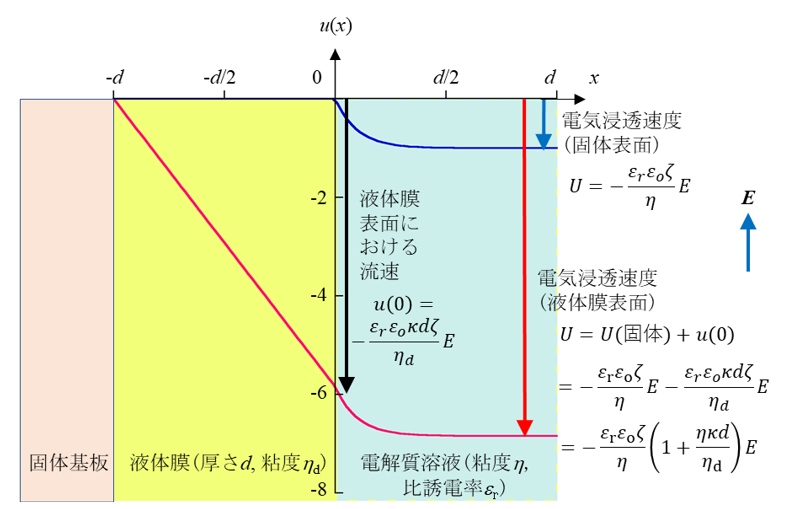
図2 水銀膜上の電気浸透流速u(x)(赤線)および固体表面上の電気浸透流速u(x)(青線)
x→∞における流速u(-∞)が電気浸透速度Uである。液体膜の粘度ηd→∞で固体になり、液体膜上の流速分布(図2の赤線)は固体表面の場合の流速分布(青線)に一致する。液体膜上の電気浸透の場合のu(x)(赤線)は電解質溶液中では指数関数的で固体表面の場合と同じである。しかし、液体膜内で液の流動が存在するために、固体表面の場合と違って、液体表面上の流速u(0)はゼロにならずに、有限の値をとる。この値u(0)が固体の場合の電気浸透速度に加算した値が液体膜上の電気浸透速度Uになり、次式で与えられる。
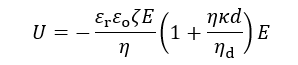 (1)
(1)液体膜上の電気浸透速度は液体膜内部に流れが存在すために、固体の場合の1+ηκd/ηd倍に増大する。

