第36回 球状高分子電解質の電気泳動:Hermans-藤田の理論
Brinkman-Debye-Buecheモデルは電気的に中性な球状高分子を対象にしているが、高分子セグメントが帯電している場合に発展させた理論がHermansと藤田による球状高分子電解質の電気泳動理論である。高分子内部に固定電荷が体積密度ρfixで一様に分布し、媒質である電解質水溶液(粘度η, 比誘電率εr)が高分子内部に浸透できる場合、Hermans-藤田の理論によれば、半径αの球状高分子電解質の電気泳動移動度μは次式で与えられる。
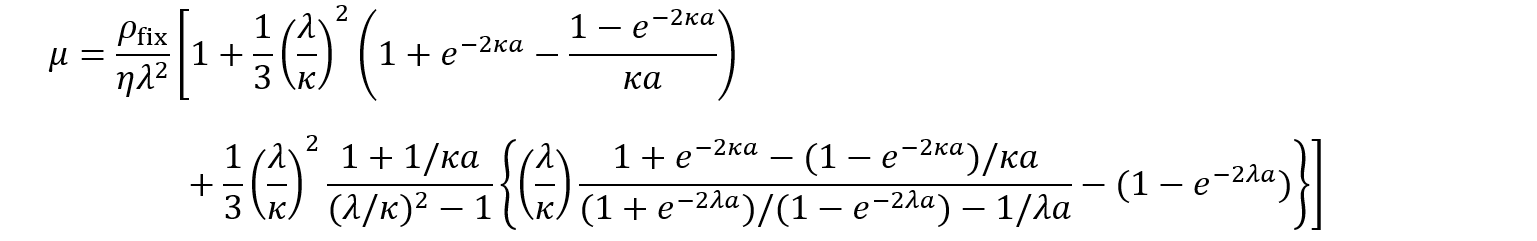 (1)
(1)1/λはBrinkmanの遮蔽長、1/κは電気二重層の厚さ(Debye長)である。(1)式にはゼータ電位ζが登場しないという点で、これまで扱った固体粒子や液滴の電気泳動移動度の式と全く異なる形をしている。その代わりに、固定電荷密度ρfixが登場する。図1にいくつかのλαに対するμのκα依存を図示したが、固体や液滴との違いがさらにはっきりする。καの小さい場合と大きい場合に塩濃度依存が小さくなりμはほぼ一定になる。
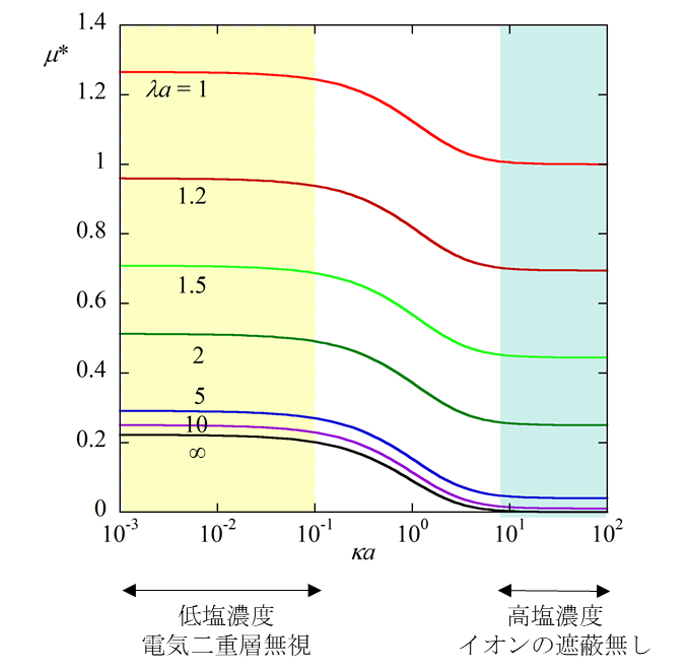
ただし、μ*=μ/(ρfixα2/η)は無次元化した電気泳動移動度. 電気浸透のため高塩濃度で泳動する。
塩濃度が低い場合は、電気二重層が消失し、固体粒子の場合のHückelの式に対応する次式になる。
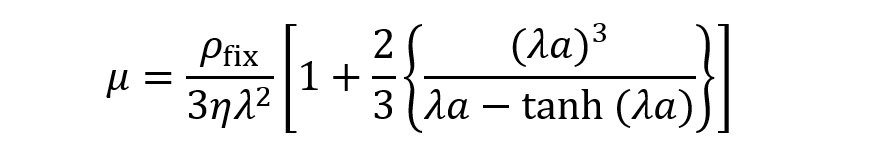 (2)
(2)(2)式は球状高分子電解質に働く電場からの力=$(4π/3) ρ_{fix}^3E$とStokes抵抗(第32回コラム(2)式)を等置すると得られる。また、高塩濃度では
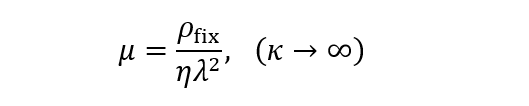 (3)
(3)になり、やはり、塩濃度に依存せず一定値である。(3)式は高分子内部を通過する電気浸透流である。固体粒子の場合、高塩濃度でμ=εrεoζ/ηになるが(εo= 真空の誘電率)、ζ自体が一般に高塩濃度でゼロに近づくので、μ→ 0となることと大きく異なる。なお、λ→ ∞では、高分子内部で電解質水溶液の流動が起こらないが、完全な固体とは異なる。なぜなら、媒質の電解質水溶液は高分子内部に侵入できるからである。この極限における電気泳動移動度は次式になる。
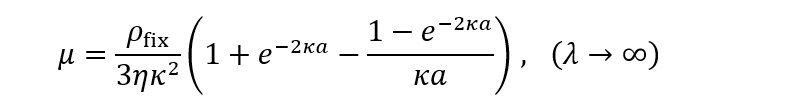 (4)
(4)実は高分子電解質の表面電位を計算すると
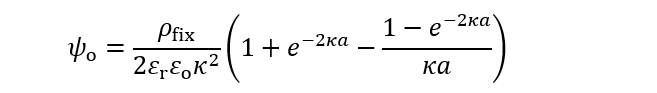 (5)
(5)になるので、(4)式は
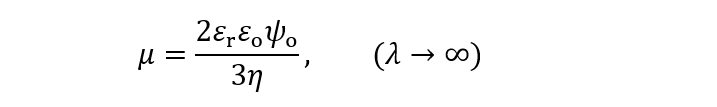 (6)
(6)となり、表面電位ψoをゼータ電位とみなせば、ちょうど、Hückelの式に一致する。有限のλの場合に対しては、 (6)式に電気浸透流の寄与((3)式)を加えた次式で良く近似できる。
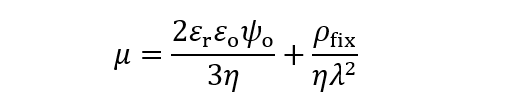 (7)
(7)
