第22回 Hückelの式

Smoluchowskiの式は電気二重層の厚さ（Debye長1/κ）に比べて大きなサイズをもつ粒子に適用される。この条件は半径αの球の場合、α»1/κ つまり κα»1である。今回は逆に粒子のサイズに比べてDebye長がはるかに大きい場合（α«1/κ つまり κα«1）の電気泳動を考える。
電解質濃度が低い場合や電解質イオンの存在が無視できるような有機溶媒系が対象である。第4回コラムで述べたように、電解質濃度を下げていくと粒子周囲のイオン雲の厚さであるDebye長が長くなり、同時にイオン雲はかすれて希薄になりついに消失する。この極限では事実上電解質濃度ゼロで電気二重層の存在しない系になる（厳密には、電解質濃度ゼロといっても、電気的中性条件から粒子の電荷に等しい量の対イオンが系内に存在しなければならない。このような系を無添加塩系、無塩系あるいは「対イオンのみ含む系」といい、対イオン凝縮現象とよばれる特異な現象を示す。これについては、後のコラムで扱う。電気二重層が存在しない場合、電場Eの下で速度Uで泳動する球状粒子（半径α）の電気泳動移動度μ= U/Eは以下のように求められる。
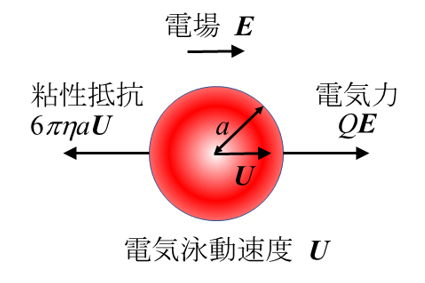
粘度η、比誘電率ε_rの液体媒質中を速度Uで動く半径αの球状粒子に働く粘性抵抗は6πηαUである（ストークス抵抗）。一方、粒子の表面電荷の総量をQとすると、粒子が電場から受ける力はQEである。電気力と粘性抵抗のつりあいの式はQE=6πηαUである。さらに、電解質濃度ゼロなので、粒子の表面電位ψ_oはクーロン電位ψ_o= Q/4πε_rε_oで与えられる（ε_o= 真空の誘電率）。この式をつり合いの式に代入すると、電気泳動移動度 μ= U/Eに対する以下の(1)式が得られる。これがHückelの式である。

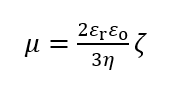(1)

Hückelの式は電解質イオンの存在しない極限の場合（κα→ 0）に導かれたが、実際にはκαが0.3以下であれば適用できる。
電場Eの下で速度Uで泳動する粒子表面周囲の流速分布u(x)と電位分布 ψ(x)を正確に計算して得られた結果を図2に示した。

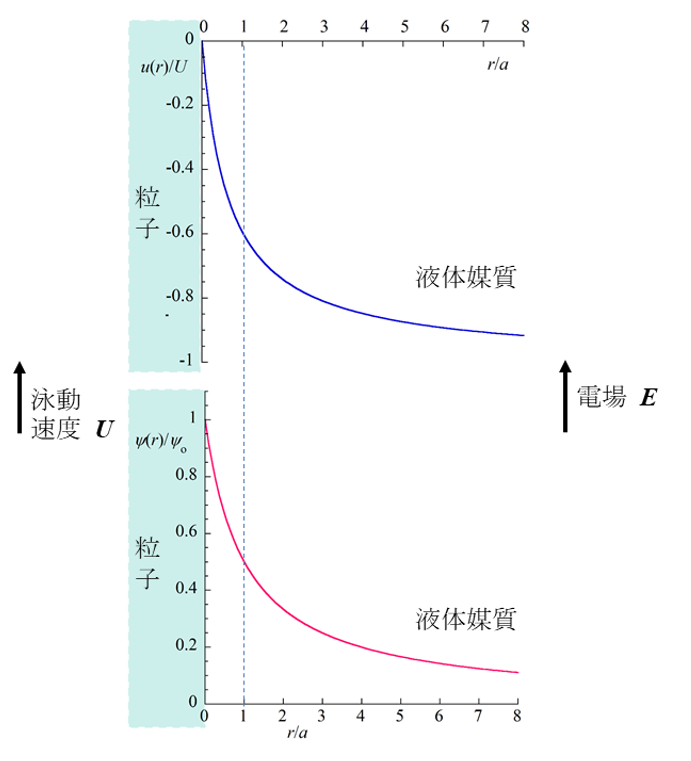
図2. 電場Eの下で速度Uで泳動する粒子表面周囲の流速分布u(x)と電位分布 ψ(x)

Hückelの式とSmoluchowskiの式（第20回コラム）を比べると係数が2/3異なる。この違いについては次回のコラムで再び取り上げるが、粒子周囲の電位分布と流速分布がκαが大きい場合（Smoluchowski）と小さい場合（Hückel）で大きく異なることに起因する。第20回と今回のコラムのそれぞれの図2を比較すると、電位と流速の変化がSmoluchowskiの場合は粒子表面周囲の厚さ1/κの狭い領域に局限されているのに対して、Hückelの場合は粒子サイズ程度の広い範囲にわたっていることがわかる。このために、Smoluchowskiの場合は粒子表面を平面とみなし粒子表面の単位面積を考えたが、Hückelの場合は粒子全体を扱ったのである。